Loans
Loans are a way for your company to raise funds in exchange for a series of repayments spread over multiple cycles. FSCharter uses an amortised loan system, which means your instalments are structured to include both interest and principal in a predictable way.
What Is Amortisation?
Amortisation is the process of spreading loan repayments evenly over a fixed term. Instead of paying just the interest each cycle and then the full amount at the end, you pay a fixed instalment (called the EMI – Equated Monthly Instalment, or more generally “per-cycle instalment”).
Each instalment is split into two parts:
Interest – calculated on the outstanding balance at the start of the cycle.
Principal – the remainder of your instalment, which reduces your loan balance.
At the beginning, the interest portion is larger (because the balance is still high). As time goes on, more of each instalment goes towards reducing the principal. This gradual shift is the defining feature of amortisation.
How FSCharter Calculates Your Loan
When you request a loan, FSCharter determines:
Principal – the amount you borrow.
Term – the number of repayment cycles.
Per-cycle interest rate (
r) – determined by the loan product and amount.Term-equivalent rate (
Rterm) – a display-only value showing the effective rate if compounded over the whole term.
Using these, FSCharter calculates your per-cycle repayment (EMI) using the standard amortisation formula:
EMI = P × (r × (1 + r)^n) / ((1 + r)^n – 1)
Where:
P= amount borrowed (principal)r= per-cycle interest raten= number of cycles in the term
If r is zero (an interest-free product), then:
EMI = P / n
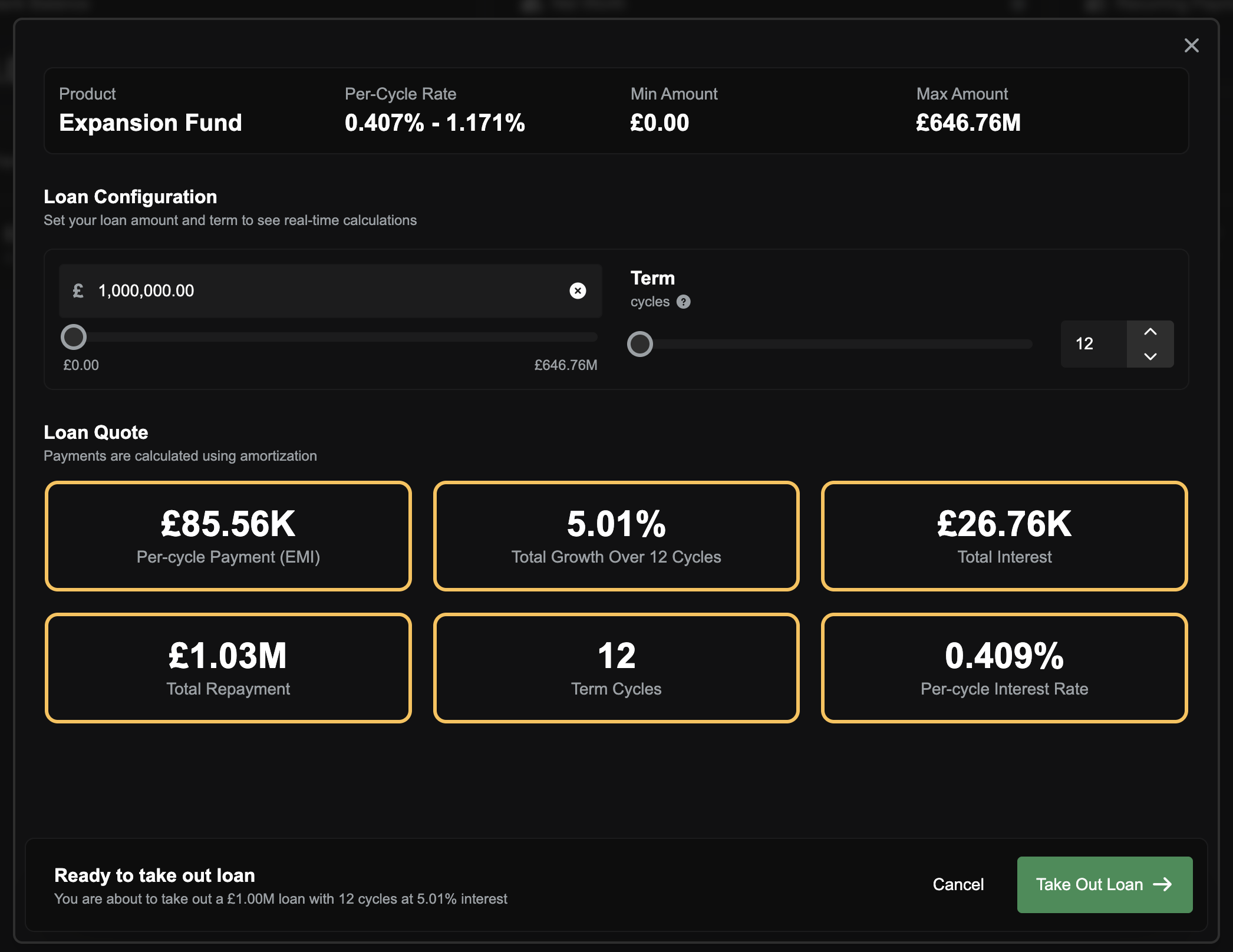
When you are configuring a new loan you can preview these figures before you commit, so you can see:
Your fixed instalment (
emi)The total repayment
The total interest
How the per-cycle rate compares to the full-term equivalent
Example Loan (No Early Repayment)
Suppose you borrow 50 million at a per-cycle interest rate of 0.8% (0.008) over 12 cycles.
Cycle | Instalment | Interest | Principal | Balance Remaining |
|---|---|---|---|---|
1 | 4.52 M | 0.40 M | 4.12 M | 45.88 M |
2 | 4.52 M | 0.37 M | 4.15 M | 41.73 M |
3 | 4.52 M | 0.33 M | 4.19 M | 37.54 M |
4 | 4.52 M | 0.30 M | 4.22 M | 33.32 M |
… | … | … | … | … |
12 | 4.52 M | 0.04 M | 4.48 M | 0.00 M |
Total repayment: ~54.3 M
Total interest paid: ~4.3 M
Notice how the interest portion shrinks each cycle, and the principal portion grows - that’s amortisation at work.
Example Loan (With Early Repayment)
Now imagine you make a 10 M lump-sum repayment at cycle 3. Your balance drops more sharply, and future interest is calculated on this lower balance.
Cycle | Instalment | Interest | Principal | Balance Remaining (Early Repay) |
|---|---|---|---|---|
1 | 4.52 M | 0.40 M | 4.12 M | 45.88 M |
2 | 4.52 M | 0.37 M | 4.15 M | 41.73 M |
3 | 4.52 M | 0.33 M | 4.19 M | 37.54 M → 27.54 M after lump sum |
4 | 4.52 M | 0.22 M | 4.30 M | 23.24 M |
5 | 4.52 M | 0.19 M | 4.33 M | 18.91 M |
… | … | … | … | … |
10 | 4.52 M | 0.03 M | 4.49 M | 0.00 M |
Loan is cleared in 10 cycles instead of 12
Total repayment: ~51.7 M
Total interest paid: ~1.7 M
That’s a saving of ~2.6 M in interest compared with sticking to the schedule.
Why Early Repayments Save Money
Because interest is based on the current balance, lowering the balance early means:
Fewer cycles of interest
Less total repayment
Often an earlier payoff date
You can read more in the Early Loan Repayment guide.
Key Points to Remember
Loans are per-cycle products; the rate you see is applied every cycle
Instalments are fixed, but the internal split between principal and interest changes over time
The earlier you reduce your balance, the more you save on interest
You can only take each loan product once
Cycles are every 40 hours of company clock time